CENTER OF DIPOLE SHIFT
We introduce here a correction in the Earth's magnetic field because, also in the approximation of a simple magnetic dipole, you must consider the fact that the center of the dipole is shifted from the center of the Earth:
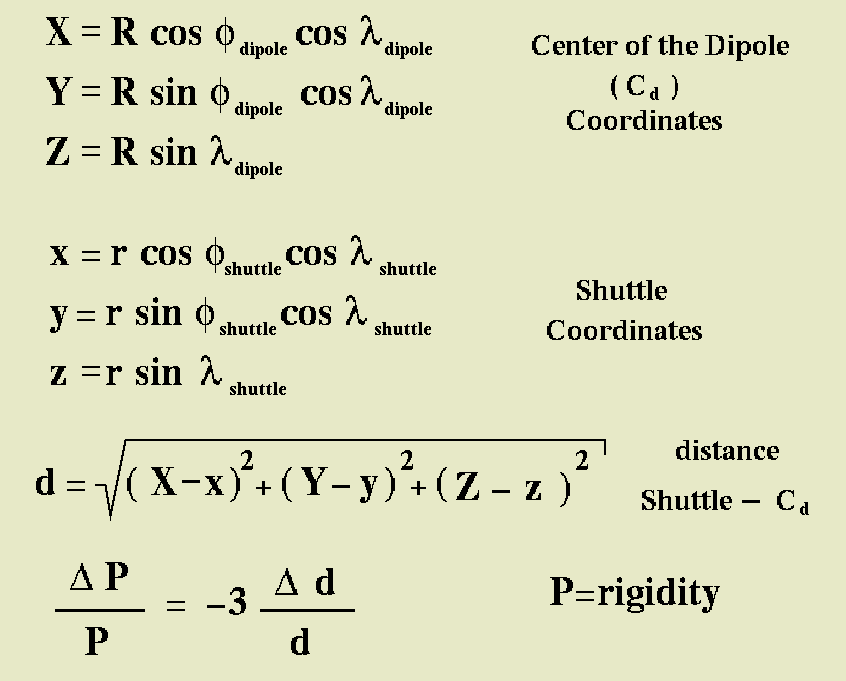
Here you can find for example the coordinates of the center of the dipole in the geographical system for year 2000:
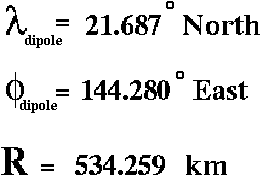
Next picture show you the relation between the Shuttle and the center of Earth's magnetic dipole, in the geographical system:
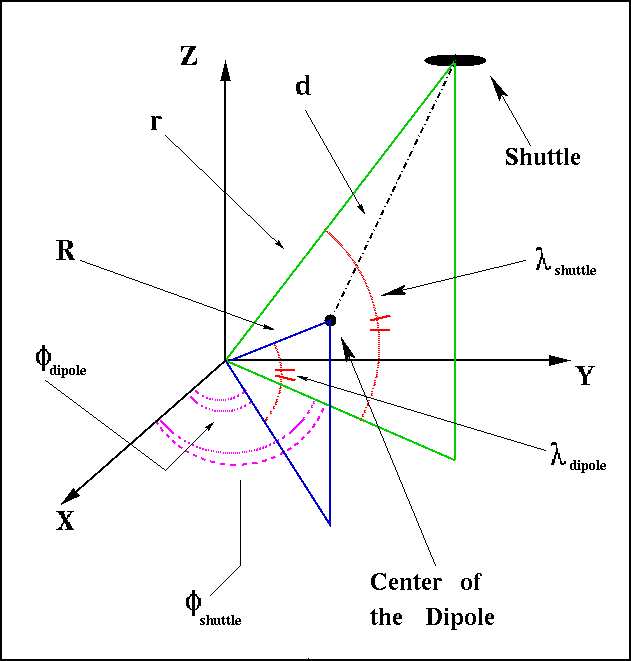
And here you can find the Stoermer equation for rigidity cut-off, for a positive particle of charge one, in the geomagnetic system, at a distance, from the center of the dipole, equal to the
earth radius (note: the East-West direction is in the geographical system of coordinates):
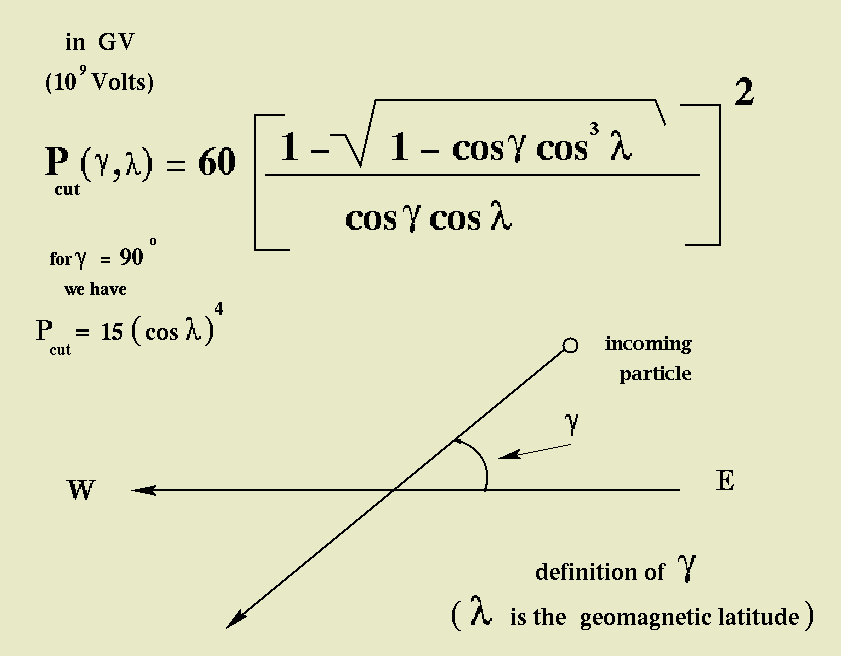
LARMOR RADIUS
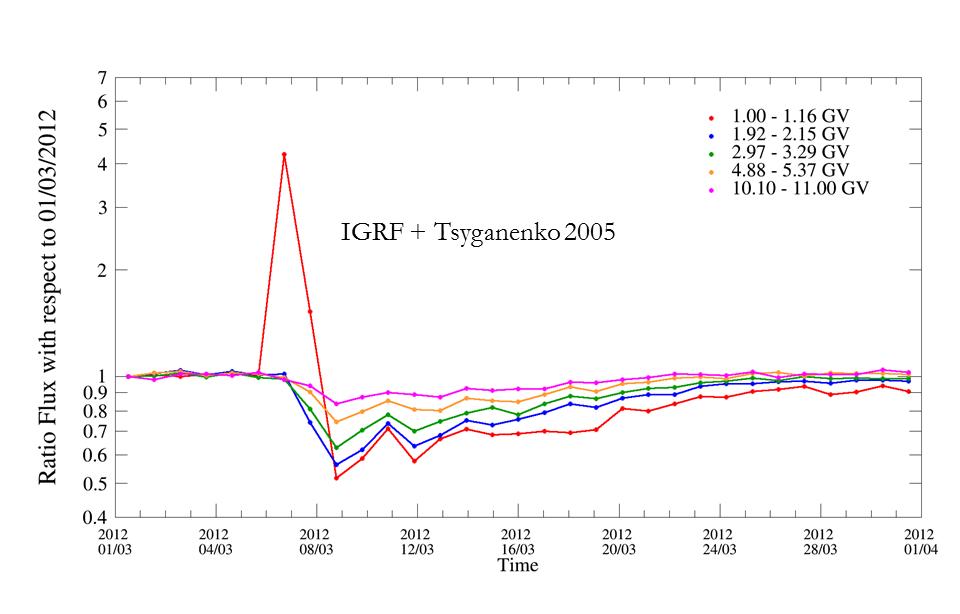
We introduce here a simple method to calculate the Larmor radius of a charged particle in space, located in the Earth's vicinity. We calculate Earth magnetic field starting from particle posistion in the shifted tilted approximation as seen below:
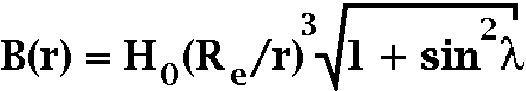
Then Larmor radius is calculated with this simple formula
![]()
and the rigidity is defined as
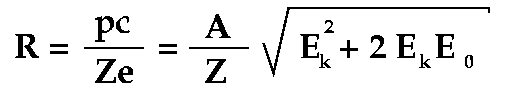
where p is the momentum, c is the speed of light, e is the electron charge, Z is the particle charge number, A is the mass number and kinetic and rest energy are per nucleon (if energy is in eV then rigidity is in Volts)