The magnetic field around the Earth, the geomagnetic field, plays an important role in the modification of the cosmic ray trajectories near Earth. It is possible to describe the main field, originated inside our planet, as a magnetic dipole with an intensity of about 0.6 G in the polar regions and about 0.3 G in the equatorial one. This field is well known on the surface, instead, the ones originated outside Earth are variable and can be superimposed to the main field; this linear summation is no more valid for distances greater than several Earth radii.
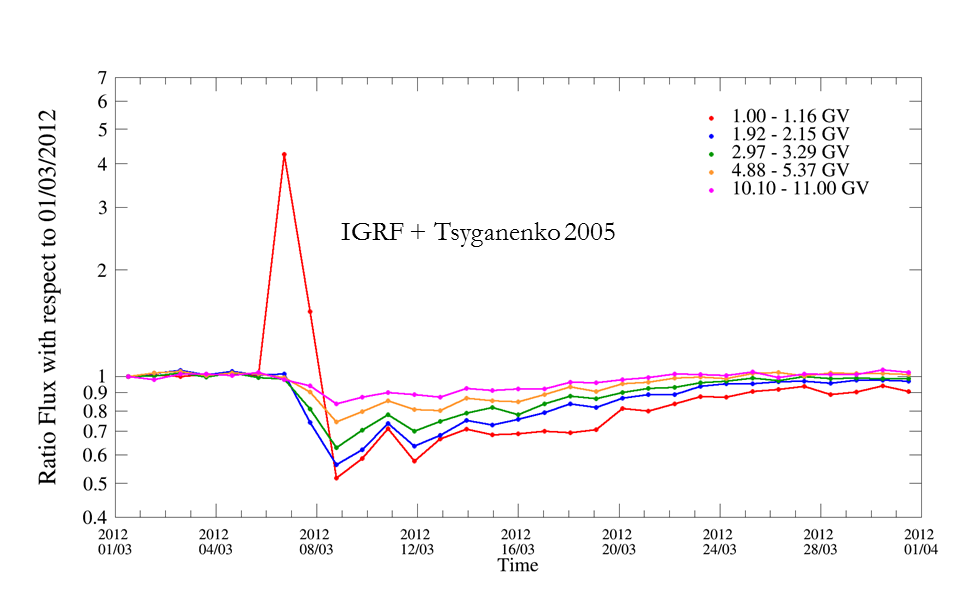
A good description of the geomagnetic field is needed for untangling primary cosmic rays (coming from the outer magnetosphere) from secondary (produced in the atmosphere) or trapped cosmic rays (in the radiation belts). The rigidity value used for discriminating these two families depends on many parameters and it is called geomagnetic rigidity cut-off, whose analytical formula was proposed by Störmer. The limit of the model is that the Störmer cut-off is not time dependent, while the magnetic field is variable (secular variation of the dipole orientation and intensity) and depending also from the solar activity.
The geomagnetic field, described as a dipole, has the center offset from the center of the Earth of about 500 km and whose axis is tilted to the rotational axis by about 11°. For this reason, magnetic poles do not coincide with the geographical ones and their positions change slowly over the years. Its intensity varies over geological time-scales and, but not regular, it is also possible to have the reverse of the polarity. This internal magnetic field is described as the negative gradient (in source free regions) of a scalar potential, that is represented by a truncated series of spherical (13th order ) harmonic expansion.
\begin{equation}
V(R,\vartheta,\lambda)=R_{E}\cdot\sum_{n+1}^{N}\sum_{m=0}^{n}\left(\frac{R_{E}}{r}\right)^{n+1}\cdot\left[g^{m}_{n}\cos(m\phi)+h^{m}_{n}\sin(m\phi)\right]\cdot P^{m}_{n}\cos(\vartheta)
\end{equation}
where \(r\) is the radial distance from the center of the Earth, \(R_E=6371\) km is the the geomagnetic conventional Earth’s mean reference spherical radius, \(\vartheta\) is the geocentric co-latitude and \(\phi\) the longitude. The functions \(P^{m}_{n}\cos(\vartheta)\) are the Schmidt quasi-normalized associated Legendre functions of degree \(n\) and order \(m\). The Gauss coefficients \(g^{m}_{n}\), \(h^{m}_{n}\) are functions of time.
The International Association of Geomagnetism and Aeronomy maintains and updates every five years a model of global field (the IGRF model). To develop it, they need satellite data and data from a network of ground-based observatories.
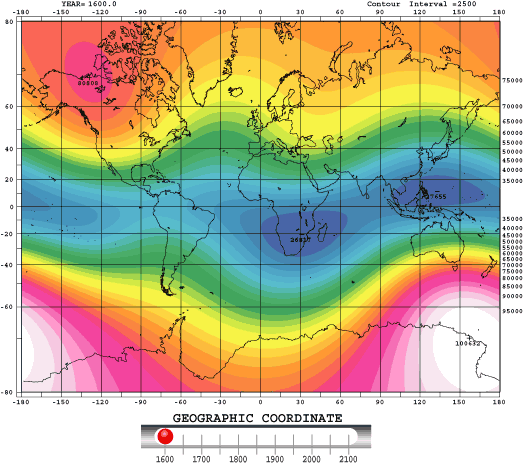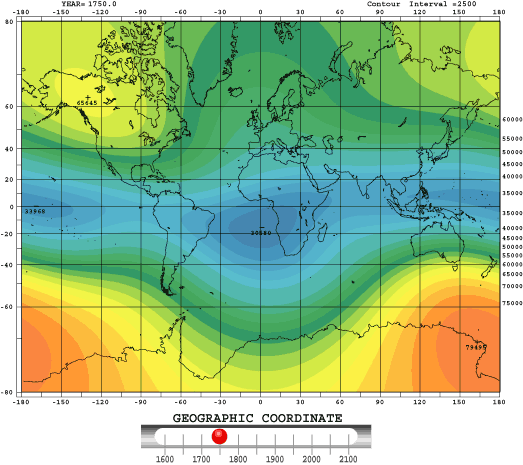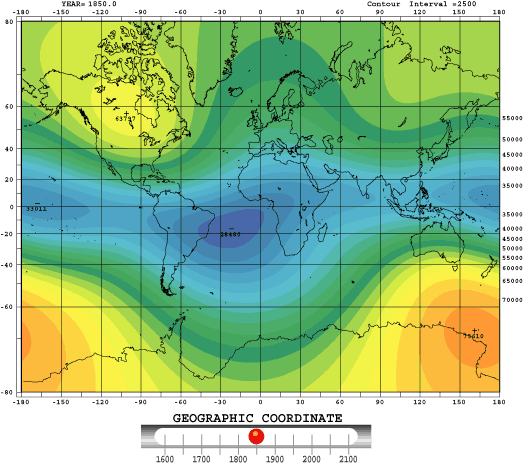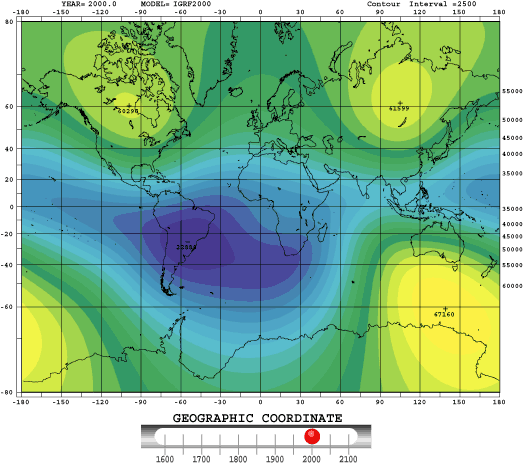
Figure 1: IGRF Magnetic Field secular variation